International Radio Alphabet
Imagine that you are the radio operator on board a motor vessel at sea in treacherous weather conditions. There is an engine failure and the ship is taking on water. The only hope is to get a message to a Coast Guard patrol boat. But the shortwave band is very noisy, your generator is down and your transmitter is running on backup batteries. It is your job to make sure your distress message gets through. But will it be correctly received and understood? Do you know your International Radio Alphabet? Your survival may depend on it.
Introduction
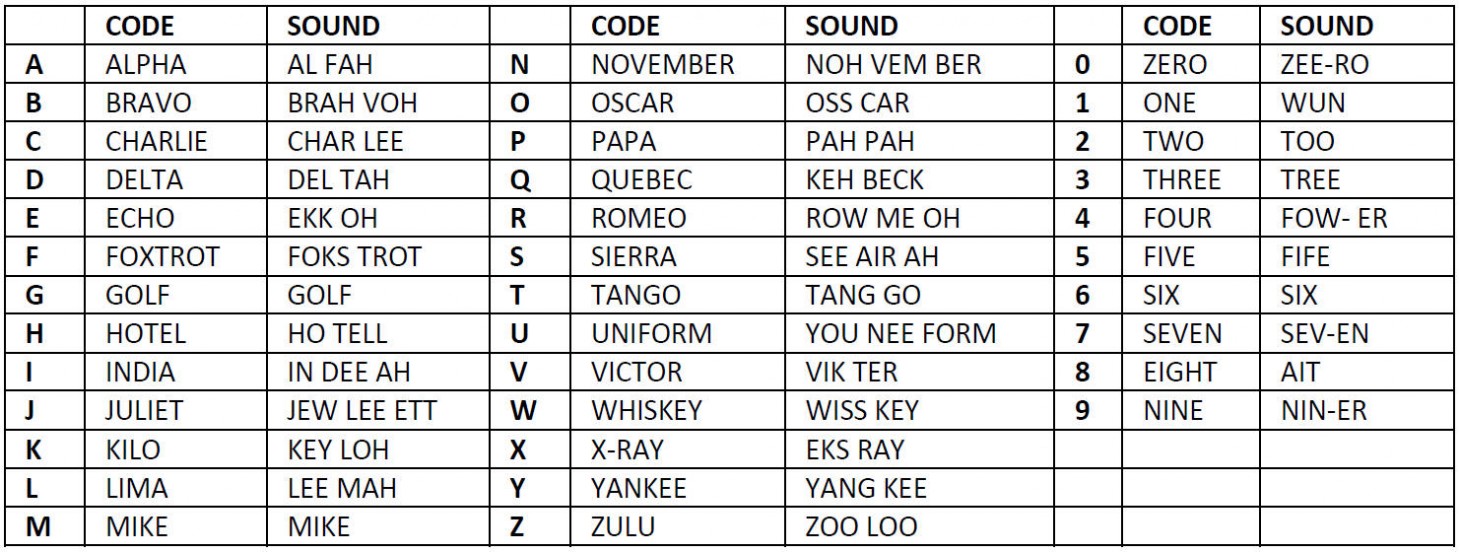
Radio operators use the International Radio Alphabet (often incorrectly referred to as a phonetic alphabet) to make sure that spoken letters and numbers don’t get lost in the noise. The sound of some letters like "F" and "S", "P" and "T" are easily confused on the air. So instead of saying “A, B, C”, radio operators use the code words “Alpha, Bravo, Charlie”, and deliberately pronounce them with clarity “AL FAH, BRAH VOH, CHAR LEE” on the air. You may be asked to spell your name or call sign "phonetically" on the air. If so you can use the following table to look up the code and sound for each letter and number. By learning these codes off by heart you gain a useful skill.
Preparation
A copy of the International Radio Alphabet table should be printed out and provided to each student. It is also available in our booklet.
Activity
- The purpose of the International Radio Alphabet and the use of the table is explained.
- Students as a group pronounce the sound of each code word from the table.
- Students take it in turns to spell their own names: E.g. "My name is Julie: JULIET UNIFORM LIMA INDIA ECHO"
- Students take it in turns to spell each other's names: E.g. "Your name is Joe: JULIET OSCAR ECHO"
- Students take it in turns to spell their club call sign: E.g. "My call sign is VK3FOWL: VICTOR KILO THREE FOXTROT OSCAR WHISKEY LIMA"


Homework
- Students spell their own names to their family members
- Students spell their family member's names
- Family members spell their own names to each other